Snake Puzzle Solver
My family know I like puzzles so they gave me this one recently:

When you take it out the box it looks like this:

And very soon after it looked like this (which explains why I've christened the puzzle "the snake puzzle"):

The way it works is that there is a piece of elastic running through each block. On the majority of the blocks the elastic runs straight through, but on some of the it goes through a 90 degree bend. The puzzle is trying to make it back into a cube.
After playing with it a while, I realised that it really is quite hard so I decided to write a program to solve it.
The first thing to do is find a representation for the puzzle. Here is the one I chose:
# definition - number of straight bits, before 90 degree bend
snake = [3,2,2,2,1,1,1,2,2,1,1,2,1,2,1,1,2]
assert sum(snake) == 27
If you look at the picture of it above where it is flattened you can see where the numbers came from. Start from the right hand side.
That also gives us a way of calculating how many combinations there are. At each 90 degree joint, there are 4 possible rotations (ignoring the rotations of the 180 degree blocks) so there are:
>>> 4**len(snake)
17179869184
17 billion combinations. That will include some rotations and reflections, but either way it is a big number.
However it is very easy to know when you've gone wrong with this kind of puzzle - as soon as you place a piece outside of the boundary of the 3x3x3 block you know it is wrong and should try something different.
So how to represent the solution? The way I've chosen is to represent it as a 5x5x5 cube. This is larger than it needs to be but if we fill in the edges then we don't need to do any complicated comparisons to see if a piece is out of bounds. This is a simple trick but it saves a lot of code.
I've also chosen to represent the 3d structure not as a 3d array but as
a 1D array (or list in python speak) of length 5 x 5 x 5 = 125.
To move in the x direction you add 1, to move in the y direction you
add 5 and to move in the z direction you move 25. This simplifies the
logic of the solver considerably - we don't need to deal with vectors.
The basic definitions of the cube look like this:
N = 5
xstride=1 # number of pieces to move in the x direction
ystride=N # number of pieces to move in the y direction
zstride=N*N # number of pieces to move in the z direction
In our list we will represent empty space with 0 and space which
can't be used with -1:
empty = 0
Now define the empty cube with the boundary round the edges:
# Define cube as 5 x 5 x 5 with filled in edges but empty middle for
# easy edge detection
top = [-1]*N*N
middle = [-1]*5 + [-1,0,0,0,-1]*3 + [-1]*5
cube = top + middle*3 + top
We're going to want a function to turn x, y, z co-ordinates into an
index in the cube list:
def pos(x, y, z):
"""Convert x,y,z into position in cube list"""
return x+y*ystride+z*zstride
So let's see what that cube looks like:
def print_cube(cube, margin=1):
"""Print the cube"""
for z in range(margin,N-margin):
for y in range(margin,N-margin):
for x in range(margin,N-margin):
v = cube[pos(x,y,z)]
if v == 0:
s = " . "
else:
s = "%02d " % v
print(s, sep="", end="")
print()
print()
>>> print_cube(cube, margin = 0)
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1
-1 . . . -1
-1 . . . -1
-1 . . . -1
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1
-1 . . . -1
-1 . . . -1
-1 . . . -1
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1
-1 . . . -1
-1 . . . -1
-1 . . . -1
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1
Normally we'll print it without the margin.
Now let's work out how to place a segment.
Assuming that the last piece was placed at position we want to place a
segment of length in direction. Note the assert to check we
aren't placing stuff on top of previous things, or out of the edges:
def place(cube, position, direction, length, piece_number):
"""Place a segment in the cube"""
for _ in range(length):
position += direction
assert cube[position] == empty
cube[position] = piece_number
piece_number += 1
return position
Let's just try placing some segments and see what happens:
>>> cube2 = cube[:] # copy the cube
>>> place(cube2, pos(0,1,1), xstride, 3, 1)
>>> print_cube(cube2)
01 02 03
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
>>> place(cube2, pos(3,1,1), ystride, 2, 4)
>>> print_cube(cube2)
01 02 03
. . 04
. . 05
. . .
. . .
. . .
. . .
. . .
. . .
>>> place(cube2, pos(3,3,1), zstride, 2, 6)
>>> print_cube(cube2)
01 02 03
. . 04
. . 05
. . .
. . .
. . 06
. . .
. . .
. . 07
The next thing we'll need is to undo a place. You'll see why in a moment.
def unplace(cube, position, direction, length):
"""Remove a segment from the cube"""
for _ in range(length):
position += direction
cube[position] = empty
>>> unplace(cube2, pos(3,3,1), zstride, 2)
>>> print_cube(cube2)
01 02 03
. . 04
. . 05
. . .
. . .
. . .
. . .
. . .
. . .
Now let's write a function which returns whether a move is valid given
a current position and a direction and a length of the segment we
are trying to place.
def is_valid(cube, position, direction, length):
"""Returns True if a move is valid"""
for _ in range(length):
position += direction
if cube[position] != empty:
return False
return True
>>> is_valid(cube2, pos(3,3,1), zstride, 2)
True
>>> is_valid(cube2, pos(3,3,1), zstride, 3)
False
Given is_valid it is now straight forward to work out what moves are
possible at a given time, given a cube with a position, a
direction and a length we are trying to place.
# directions next piece could go in
directions = [xstride, -xstride, ystride, -ystride, zstride, -zstride]
def moves(cube, position, direction, length):
"""Returns the valid moves for the current position"""
valid_moves = []
for new_direction in directions:
# Can't carry on in same direction, or the reverse of the same direction
if new_direction == direction or new_direction == -direction:
continue
if is_valid(cube, position, new_direction, length):
valid_moves.append(new_direction)
return valid_moves
>>> moves(cube2, pos(3,3,1), ystride, 2)
[-1, 25]
So that is telling us that you can insert a segment of length 2 using a
direction of -xstride or zstride. If you look at previous
print_cube() output you'll see those are the only possible moves.
Now we have all the bits to build a recursive solver.
def solve(cube, position, direction, snake, piece_number):
"""Recursive cube solver"""
if len(snake) == 0:
print("Solution")
print_cube(cube)
return
length, snake = snake[0], snake[1:]
valid_moves = moves(cube, position, direction, length)
for new_direction in valid_moves:
new_position = place(cube, position, new_direction, length, piece_number)
solve(cube, new_position, new_direction, snake, piece_number+length)
unplace(cube, position, new_direction, length)
This works by being passed in the snake of moves left. If there are no
moves left then it must be solved, so we print the solution. Otherwise
it takes the head off the snake with
length, snake = snake[0], snake[1:] and makes the list of valid moves
of that length.
Then we place each move, and try to solve that cube using a
recursive call to solve. We unplace the move so we can try again.
This very quickly runs through all the possible solutions:
# Start just off the side
position = pos(0,1,1)
direction = xstride
length = snake[0]
# Place the first segment along one edge - that is the only possible place it can go
position = place(cube, position, direction, length, 1)
# Now solve!
solve(cube, position, direction, snake[1:], length+1)
Solution
01 02 03
20 21 04
07 06 05
16 15 14
19 22 13
08 11 12
17 24 25
18 23 26
09 10 27
Solution
01 02 03
16 15 14
17 24 25
20 21 04
19 22 13
18 23 26
07 06 05
08 11 12
09 10 27
Wow! It came up with 2 solutions! However they are the same solution just rotated and reflected.
But how do you use the solution? Starting from the correct end of the snake, place each piece into its corresponding number. Take the first layer of the solution as being the bottom (or top - whatever is easiest), the next layer is the middle and the one after the top.
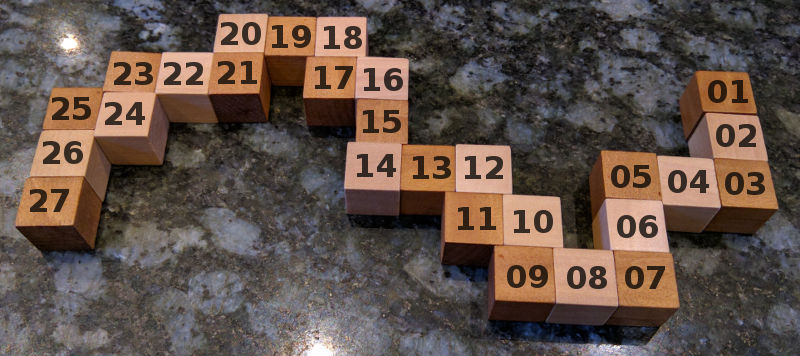
After a bit of fiddling around you'll get...

I hope you enjoyed that introduction to puzzle solving with computer.
If you want to try one yourselves, use the same technique to solve solitaire.
Download the entire code snake_puzzle_solver.py or the iPython notebook.